[데이터베이스설계론] 6주차 수업 내용 정리
6주차 수업 내용 정리
데이터 조작 개본 개념
데이터 조작
- 데이터베이스에 질문, 검색, 조회(쿼리) 수행
- 사용자가 관계형 데이터베이스에 데이터 조작 언어를 사용해 질문을 수행하고, 원하는 결과를 획득함
- 예시: 전체 직원 정보 테이블에서, 급료가 50 이상인 사원만을 검색

- 사용자가 관계형 데이터베이스에 데이터 조작 언어를 사용해 질문을 수행하고, 원하는 결과를 획득함
- 데이터베이스를 업데이트
- 튜플 삽입 insert
- 예시: 새로운 사원의 정보를 데이터베이스에 삽입
- 튜플 삭제 delete
- 예시: 기존 사원의 정보를 데이터베이스에서 삭제
- 튜플 수정 rewrite, modification, update
- 예시: 기존 사원의 정보 일부를 변경
- 튜플 삽입 insert
관계의 조작
- 관계대수와 관계논리
- 둘 모두 Codd 박사에 의해 제안됨
- 관계대수 関係代数 Relational Algebra
- 관계에 대한 조작 순서를 기술 -> 어떠한 처리를 행할 것인가?
- 집합 연산과 특유 연산
- 집합 연산 Set Operations: 합집합, 곱집합, 차집합, 데카르트곱 集合差
- 특유 연산: 사영 射影(필드 추출), 선택 選択(조건에 따른 튜플 선택), 제약 制約, 조인 結合(결합), 나눗셈(商 연산)
- 관계논리 関係論理 Relational Calculus
- 출력하고자 하는 관계를 논리식으로 기술
- 어떤 조건의 데이터를 원하는가?
- 기호 논리를 이용
- 변수, 기호: x, y, R, S, …
- 부정: ¬
- 논리곱:∧
- 논리합:∨
- 전칭 全称(모든 ~에 대해), 존재 存在(어떤 ~가 존재한다면): ∀・∃
- 예시:
∀x P(x): 모든 x에 대해 P(x)가 성립,∃x P(x): 어떤 x에 대해 P(x)가 성립
- 예시:
- 출력하고자 하는 관계를 논리식으로 기술
관계대수
- 집합 연산 Set Operations: 합집합, 교집합, 차집합, 데카르트곱 集合差
- 특유 연산: 사영, 선택, 제약, 결합, 나눗셈
- 그 외 분류
- 단항 연산
- 사영, 선택, 제약
- 이항 연산
- 합집합, 교집합, 차집합, 데카르트곱, 결합, 나눗셈
- 단항 연산
합병 가능성 Union Compatioble 조건
- 이항 연산의 두 입력에 대해
- 속성 수와 대응하는 속성의 정의역이 일치해야 한다는 조건이 존재
- 조건 성립이 필요한 연산
- 합집합, 교집합, 차집합
- 조건 성립이 불필요한 집합
- 데카르트곱, 결합, 나눗셈
-
예시: 테니스부원
Rₐ과 축구부원Rᵦ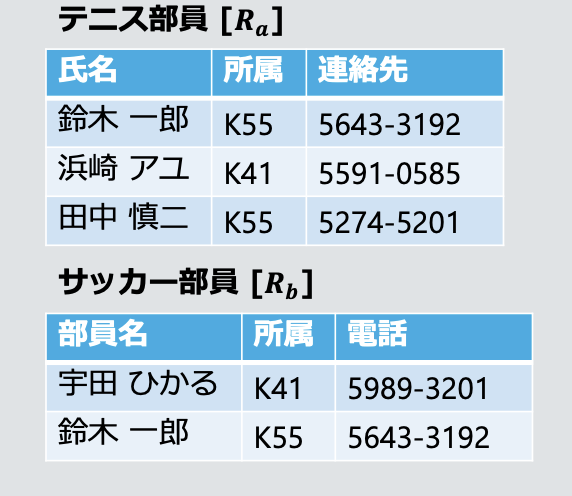
- 합병 가능 조건
- 속성 수(차수 次数)가 양쪽 동일하게 3이어야 함
dom(氏名)=dom(部員名),dom(連絡先)=dom(電話)-
dom(테니스부원, 소속)=dom(축구부원, 소속)
- **합집합 연산 Union:
Rₐ ∪ Rᵦ- 중복 제거가 필요한 경우: 카디널리티 3 + 2 vs. 4
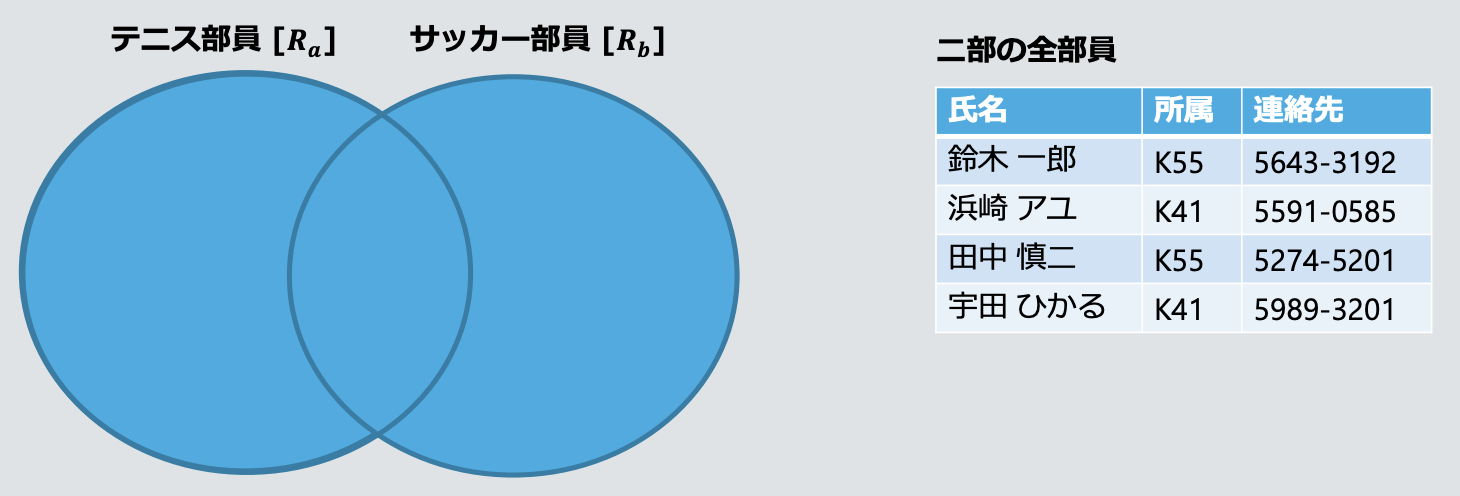
- 교집합 연산 Intersection:
Rₐ ∩ Rᵦ- 두 집합에서 공통되는 튜플
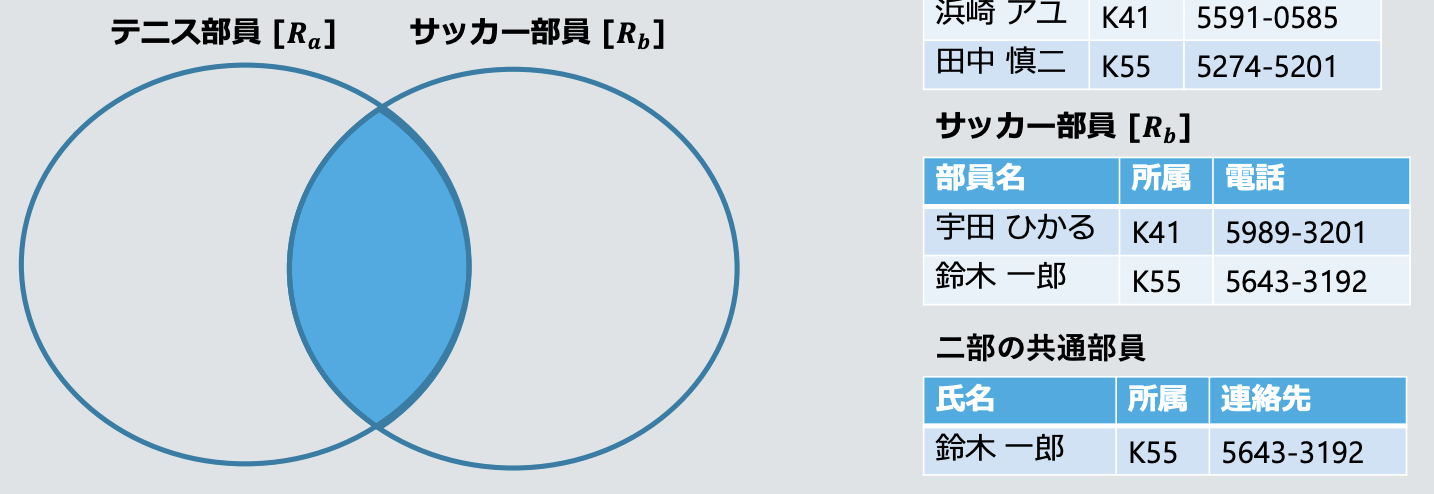
- **차집합 연산 Difference:
Rₐ − Rᵦ- Rᵦ에는 존재하지 않고, Rₐ에만 존재하는 튜플
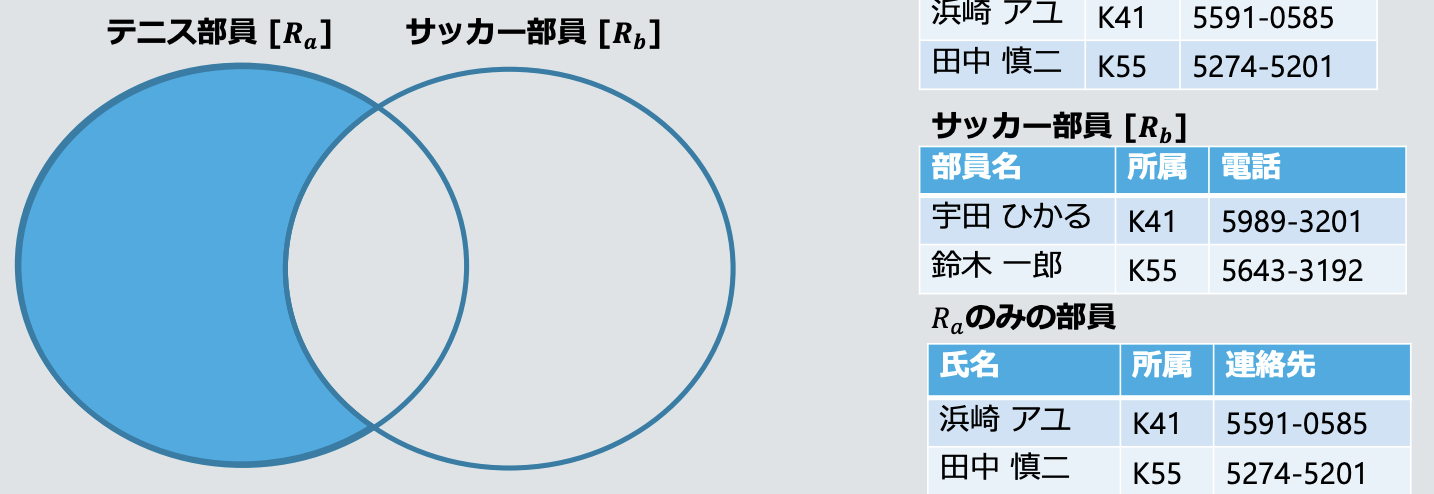
- 합병 가능 조건
-
예시: 학생
Rx과 과목Ry- 데카르트곱 연산:
Rx × Ry- 카디널리티
card(Rx × Ry) = card(Rx) × card(Ry)
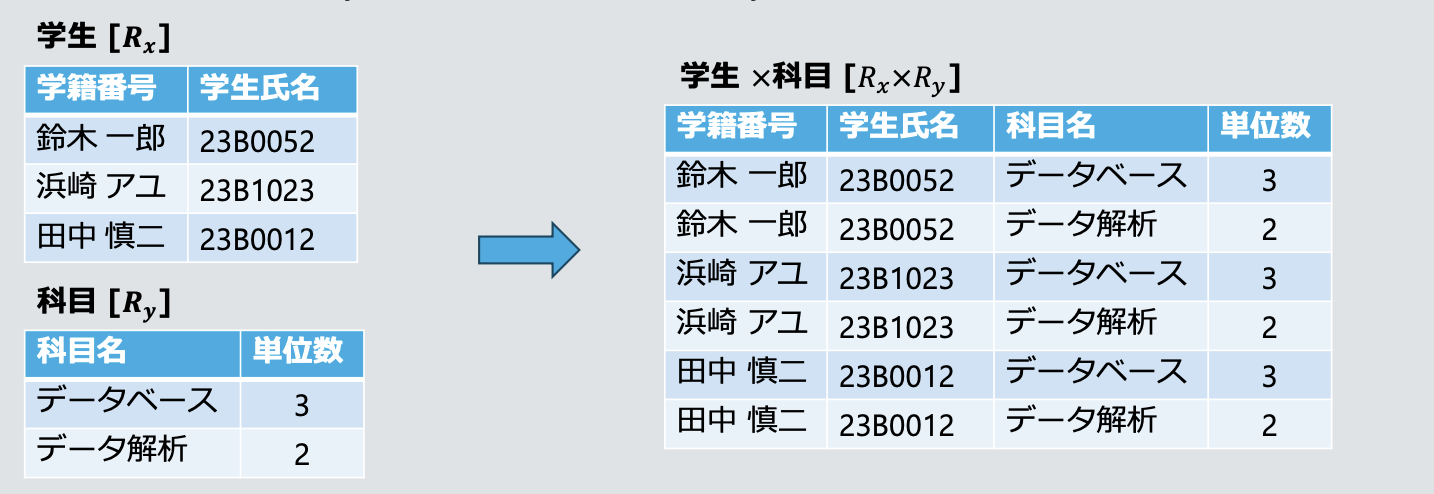
- 카디널리티
- **사영 연산 Projection:
π- 지정된 속성(A1, A2, ⋯ , An)의 추출
π A1, A2, ⋯, An(R)
- 중복 제거를 하지 않는 사영 연산을 델타 사영 Delta Projection이라고 함
- 테니스 부원
Ra로부터π 氏名(テニス部員)만을 추출
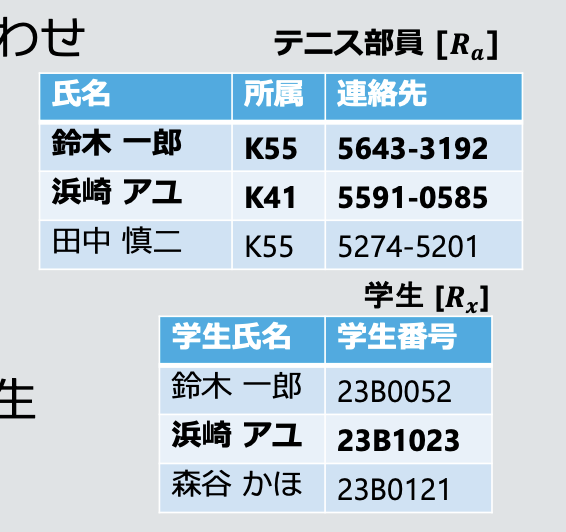
- 지정된 속성(A1, A2, ⋯ , An)의 추출
- 선택 Selection:
σ- 릴레이션 R 내의 조건
(A = α)에 맞는 튜플의 탐색- 예시:
σ 所属 = K55(テニス部員)
- 예시:
- θ 선택 θ-selection:
σ Aθα (R)- 조건의 일반화
- θ = =, ≠, <, ≤, >, ≥
- 예시:
σ 単位数 > 2(科目)
- 제약 Restriction:
σ Ai θ Aj (R)- 속성 간 조건으로 검색함
- 조건을
∧(and),∨(or)로 결합할 수 있음
- 릴레이션 R 내의 조건
- 데카르트곱 연산:
-
예시: 테니스 부원
Ra과 학생Rx
- 결합 연산 Join:
⨝- 내부 결합 Inner Join
- 두 릴레이션 간 속성 동치 조건에 따른 튜플 결합
- θ 결합 (θ-Join):
Rₐ ⨝_{Aᵢ θ Aⱼ} Rᵦ- θ: =, ≠, <, ≤, >, ≥
- 등결합 (Eq-Join)
- θ가
=일 경우:Rₐ ⨝_{Aᵢ = Aⱼ} Rᵦ
- θ가
- 예시:
テニス部員 ⨝ 氏名 = 学生氏名 学生
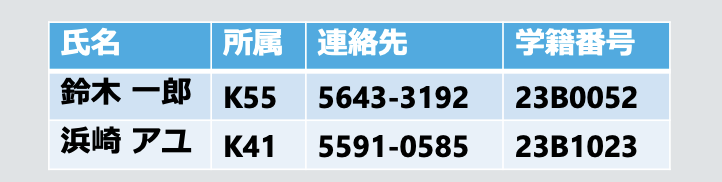
- 내부 결합 Inner Join
- 결합 연산 Join:
-
예시: 작가
Rm과 배우Rn- Eq-Join 이외의 결합(비등결합 Join)
- θ 결합을 통해 등호 외의 조건(>, < 등)을 사용한 튜플 결합을 수행함
- 예시:
Rₘ ⨝_{Rₘ.生年 > Rₙ.生年} Rₙ
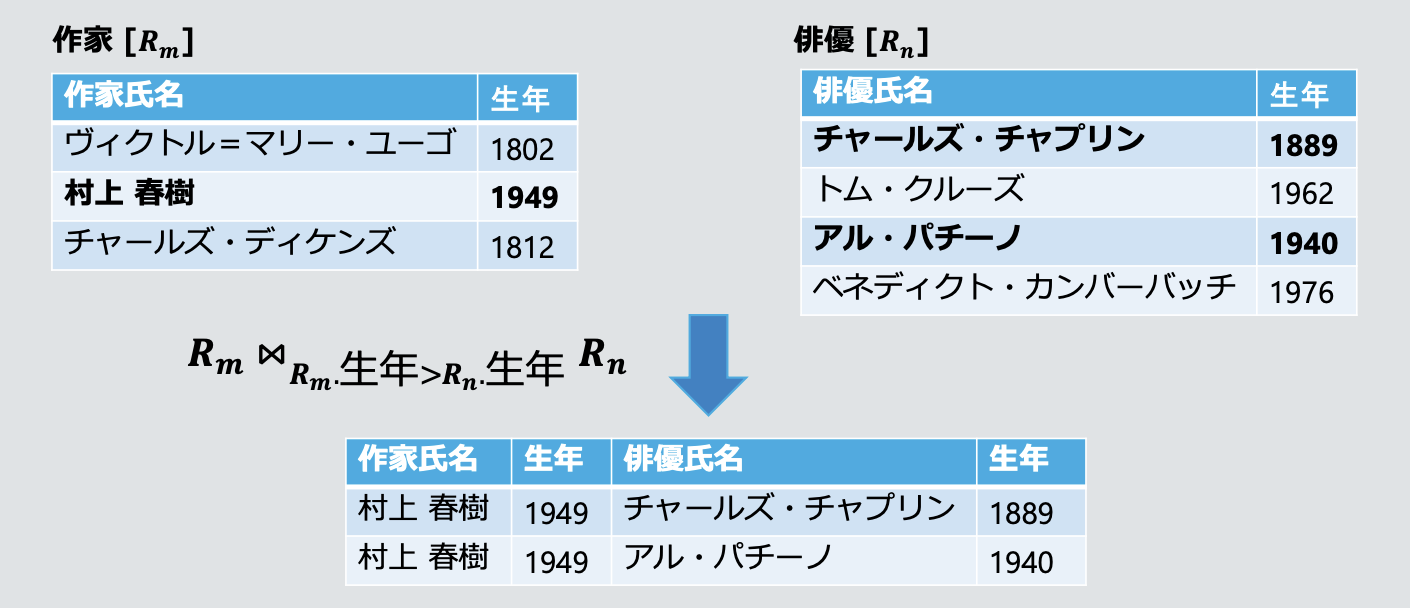
- Eq-Join 이외의 결합(비등결합 Join)
결합 연산 보충 정리
- 결합 연산의 법칙
- 교환 법칙 (Commutative law)
R ⨝ S = S ⨝ R
- 결합 법칙 (Associative law)
R ⨝ (S ⨝ T) = (R ⨝ S) ⨝ T
- 교환 법칙 (Commutative law)
- 결과는 동일하지만, 처리 비용은 달라짐
- 결합 연산은 일반적으로 비용이 높음
- RDBMS는 쿼리에 대해 복수의 비용 계획(cost plan)을 시뮬레이션하고 최적의 계획을 선택해 실행함 (※이 부분은 강의 범위 외)
- θ 결합은 데카르트곱 연산과 제약 연산, 또는 선택 연산으로 표현 가능함
- 즉 결합 Join = 데카르트곱 + 조건 필터링(Selection/Restriction)
- 예시:
R ⨝ {A = B} S ≡ σ {A = B}(R × S)
- 자연 결합 ⾃然結合 Natural Join
- 동일한 이름을 가진 속성에 대해 결합:
R * S
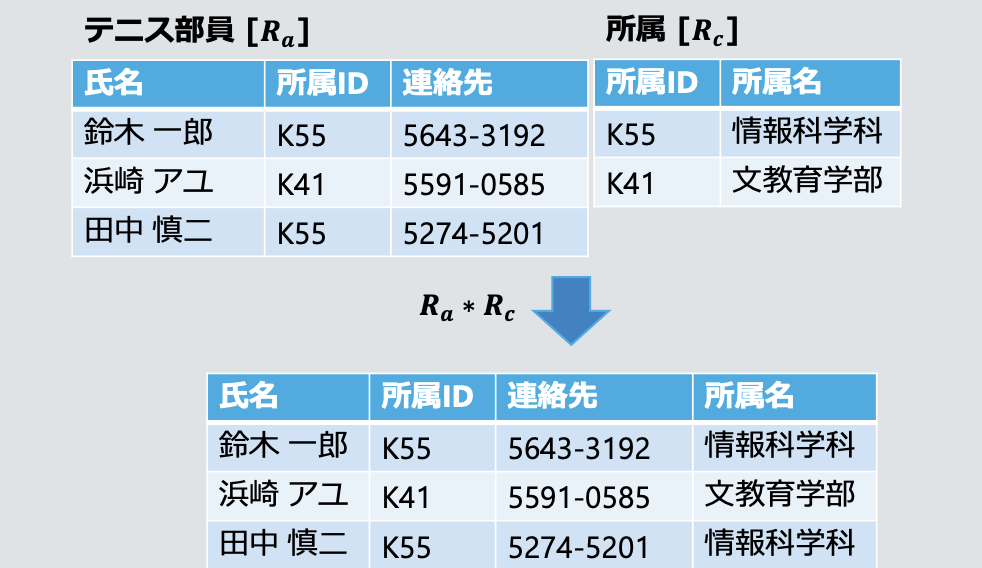
- 동일한 이름을 가진 속성에 대해 결합:
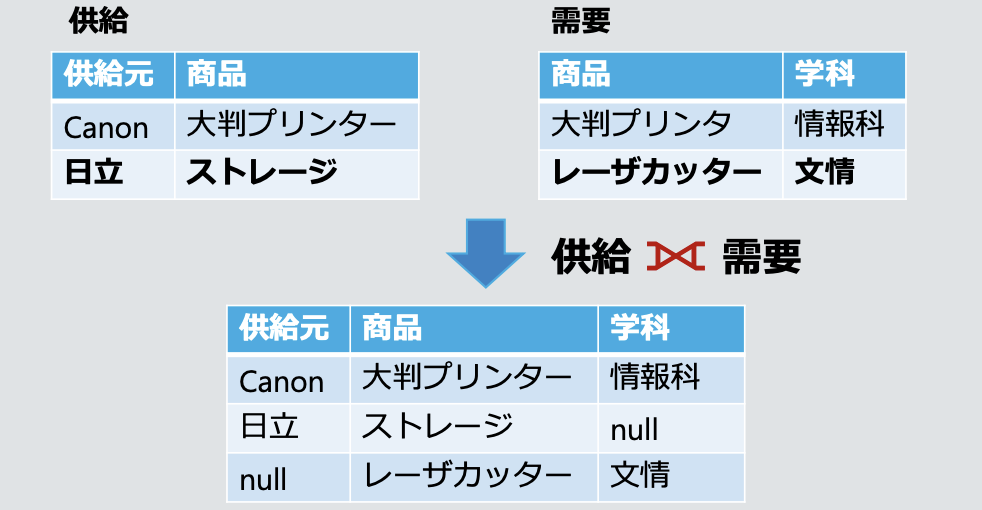
외부 결합 外結合 Outer Join
- 한쪽 테이블에 대응하는 속성값이 존재하지 않을 경우, null을 삽입함
- 아래 경우, 상품 속성에 따라 자연결합할 경우 생략되는 정보가 발생함
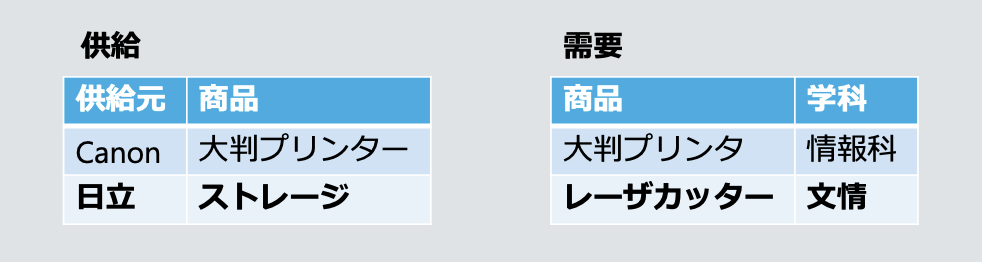
- 왼쪽 외부 결합 左外結合 Left Outer Join
- 왼쪽 테이블의 모든 튜플을 남기고, 오른쪽 테이블에 대응하는 튜플이 없으면 null로 채움
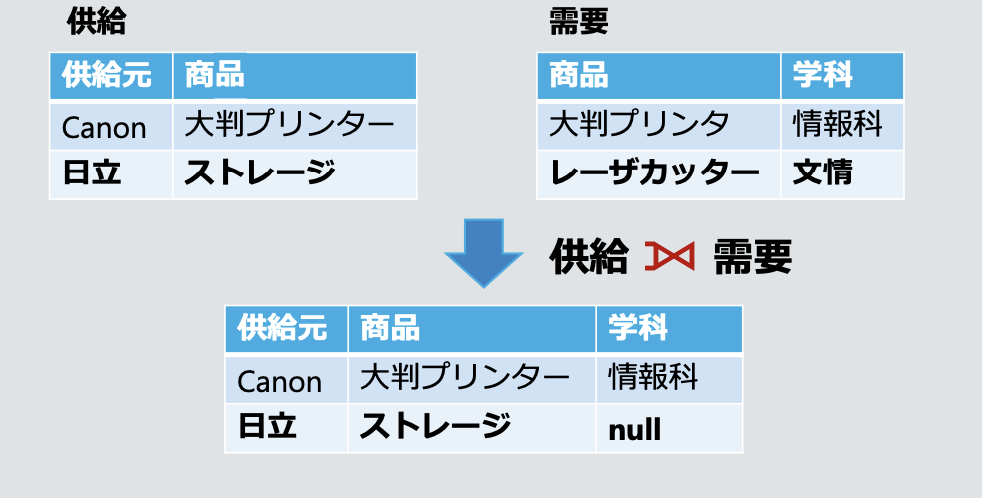
- 오른쪽 외부 결합 右外結合 Right Outer Join
- 오른쪽 테이블의 모든 튜플을 남기고, 왼쪽 테이블에 대응하는 튜플이 없으면 null로 채움
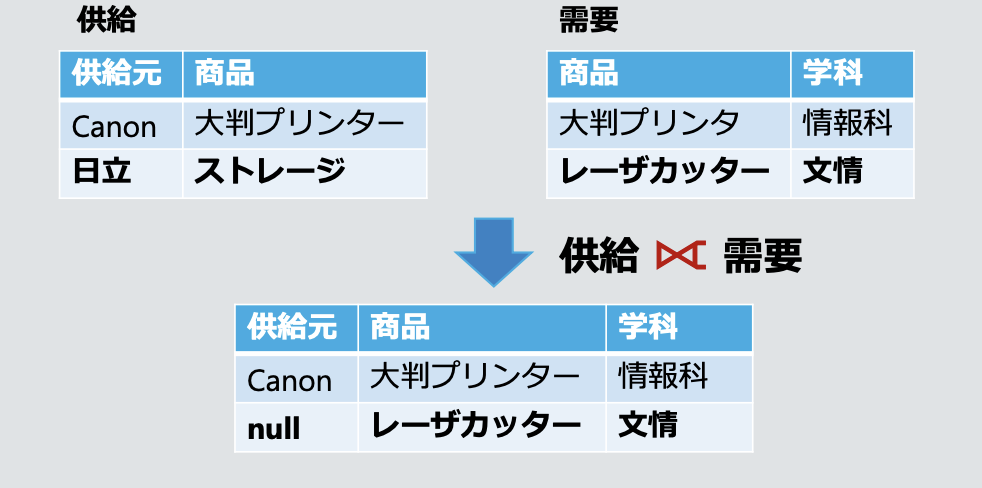
- 전체 외부 결합 全外結合 Full Outer Join
- 양쪽 테이블의 모든 튜플을 남기고, 대응하는 값이 없는 경우 null로 채움
나눗셈
Ra[X] % Rb[Y]- 테이블 Ra의 튜플 집합 중에서, 테이블 Rb의 모든 튜플의 속성을 포함하는 튜플을 모두 추출

쿼리 트리
- 일반적인 관계 대수와 질의는 최종 결과를 루트로 하는 트리 구조를 구성
- 노드는 관계 대수 연산자이며, 입력과 출력도 관계(릴레이션)이다
- 이항 연산이 분기
- 결합 연산의 교환 법칙성과 결합 법칙성에 따라 최적화가 가능
- 어떤 구조가 최적인지는 조건에 따라 달라짐
- 각 연산(특히 결합 연산)을 실제로 구현하는 알고리즘이 존재
- 각 관계의 카디널리티(튜플 수)
- 어떤 구조가 최적인지는 조건에 따라 달라짐
관계논리
집합의 표현 방법
- 외연 표현 外延表現 Extensional Expression
{2, 3, 4, 5}- 실제 원소를 명시적으로 나열
- 내포 표현 内包表現 Intensional Expression
{x | x는 정수이고, x > 1, x < 6}- 조건을 통해 원소의 성질을 기술
- 관계 논리
- 검색 결과로 얻어지는 릴레이션의 내용에 대한 내포 표현
- 출력으로 원하는 릴레이션의 조건을 논리식으로 기술
- 어떤 조건의 데이터를 원하는지를 선언적으로 명시
- 출력으로 원하는 릴레이션의 조건을 논리식으로 기술
- 다루는 방식에 따라 두 종류로 나뉨
- 튜플 관계 해석 Tuple Relational Calculus
- 튜플 변수 Tuple variable를 사용함
- 도메인 관계 해석 Domain Relational Calculus
- 도메인 변수 Domain variable를 사용함
- 이 강의에서는 다루지 않음
- 튜플 관계 해석 Tuple Relational Calculus
- 검색 결과로 얻어지는 릴레이션의 내용에 대한 내포 표현
관계논리의 정의
- 원시 논리식 原始論理式 Atomic Formula
- R, t를 각각 릴레이션 이름과 튜플 변수라고 하면,
R(t)는 원시 논리식- 이는
t ∈ R과 동의어
- 이는
- t₁, t₂를 튜플 변수, A₁, A₂를 속성명, θ를 산술 비교 연산자라고 하면,
t₁[A₁] θ t₂[A₂]는 원시 논리식- 예시:
t1[age] > t2[age]
- 예시:
- R, t를 각각 릴레이션 이름과 튜플 변수라고 하면,
- 튜플 관계 논리식 タプル関係論理式 Tuple Relational Calculus
- 원시 관계 논리식은 튜플 관계 논리식
- P₁, P₂가 튜플 관계 논리식이라면,
P₁ ∧ P₂,P₁ ∨ P₂,¬P₁또한 튜플 관계 논리식 - P가 튜플 관계 논리식이라면,
∀t P,∃t P(모든 튜플 t에 대해 P, 어떤 튜플 t가 존재해서 P) 역시 튜플 관계 논리식 - 이외의 비논리식 표현은 튜플 관계 논리식이 아님
관계대수와 관계논리의 등가성
- 집합 합 Union
P ∪ Q = {t | P(t) ∨ Q(t)}- P 또는 Q에 속하는 튜플 t의 집합
- 집합 교 Intersection
P ∩ Q = {t | P(t) ∧ Q(t)}- P와 Q 모두에 속하는 튜플 t의 집합
- 집합 차 Difference
P − Q = {t | P(t) ∧ ¬Q(t)}- P에는 속하지만 Q에는 속하지 않는 튜플 t의 집합
- 데카르트 곱 Cartesian Product
P × Q = {(t₁, t₂) | P(t₁) ∧ Q(t₂)}- P의 튜플 t₁와 Q의 튜플 t₂를 모두 조합한 튜플 쌍의 집합
- 사영 射影 Projection
π {A₁, A₂, ..., Aₙ}(R) = { t[A₁, A₂, ..., Aₙ] | R(t) }- 릴레이션 R에서 속성 A₁, A₂, …, Aₙ만 추출한 튜플들의 집합
- 선택 選択 Selection
σ {A θ α}(R) = { t | R(t) ∧ t[A] θ α }- 릴레이션 R에서 조건을 만족하는 튜플들만 추출
- 제약 制約 Restriction
σ {Aᵢ θ Aⱼ}(R) = { t | R(t) ∧ t[Aᵢ] θ t[Aⱼ] }- 속성 A의 값이 도메인에 포함되는 제한 조건이 있는 선택
- 결합 結合 Join
Rₐ ⋈_{Aₐ θ A_b} R_b = { (tₐ, t_b) | Rₐ(tₐ) ∧ R_b(t_b) ∧ tₐ[Aₐ] θ t_b[A_b] }- 두 릴레이션 R과 S에서 결합 조건을 만족하는 튜플 쌍을 연결한 결과
