[컴퓨터아키텍처] 3주차 수업 내용 정리
2진수 또는 16진수에 의한 숫자 표현
표현 방법
- 앞으로의 강의에서는 C언어의 표현 방식에 따라 표현할 것
- 10진수: 아무것도 붙이지 않음 (
143) - 2진수: 선두에
0b를 붙임 (0b10000011) - 16진수: 선두에
0x를 붙임 (0x83)
- 10진수: 아무것도 붙이지 않음 (
- 참고:
0b와 같은 2진수 표기는 C 23, C++ 14에서부터 도입되었음
현대 컴퓨터는 기본적으로 2진수 베이스로 이루어져 있음
- 전압이 높으면 1, 낮으면 0이라는 상태를 2진수로 표현하고 있음
- 가끔 1과 0의 할당이 반대가 되는 경우도 존재
- 왜 2진수인가?
- 회로의 작성이 간단하기 때문
- 예를 들어 3진수일 경우,
- 전압이 ‘높음’, ‘중간’, ‘낮음’의 3개를 구별하는 것이 됨
- 이러한 판별은, 단순히 높고 낮음으로 구별하는 것보다 복잡하고 어려움
정보 분야에서는 2진수/16진수/10진수가 섞여 나오는 일이 많음
- 이들은 단순히 표현 방법이 다를 뿐
-
표현 방법이 다를 뿐, 그것이 가리키는 숫자 그 자체는 동일함
- 왜 섞어 쓰는가?
- 10진수
- 인간이 평소 사용하고 있어, 이해하기 쉬움
- 2진수
- 컴퓨터는 2진수의 형태로 숫자를 유지하고 있음
- 2진수의 각 자릿수에 의미를 두는 경우가 많음
- 이진수 표기하는 것이 여러 가지로 생각하기 쉬움
- 4비트 데이터는 0b0000부터 0b1111까지, 즉 0부터 15까지를 표현할 수 있음
- 2진수에서 아래에서 세 번째 비트가 add/sub를 나타내는 방식
- 2진수의 경우: 세 번째 비트만 보면 판별이 가능한 방식
- add: 0bx1xx (x는 0 또는 1의 임의값)
- sub: 0bx0xx
- 10진수의 경우: 의미를 파악하기 어려운 방식
- add: 4, 5, 6, 7, 12, 13, 14, 15 중 하나인 경우
- sub: 0, 1, 2, 3, 8, 9, 10, 11 중 하나인 경우
- 2진수의 경우: 세 번째 비트만 보면 판별이 가능한 방식
- 2진수의 결점
- 인간이 이해하기 어려움
- 자릿수가 길어지기 쉬움
- 컴퓨터는 2진수의 형태로 숫자를 유지하고 있음
- 16진수
- 10진수의 0~15를 0x0, 0x1, 0x2, 0x3, 0x4, 0x5, 0x6, 0x7, 0x8, 0x9, 0xa, 0xb, 0xc, 0xd, 0xe, 0xf로 나타냄
- 이점
- 표기상 자릿수가 적어 2진수보다는 인간이 이해하기 쉬움
- 2진수와 16진수는 상호 변환이 간단함
- 10진수
- 2진수와 16진수의 상호 변환
- 2진수의 4자리와 16진수의 1자리가 1:1로 직접 대응함
- 2진수: 0b 1101 0100 1000 0111
- 16진수: 0x D 4 8 7
- 10진수: 54407
- 2진수를 4자리씩 나누어 대응시키면 간단히 변환 가능함
- 10진수와의 상호 변환은 상당한 어려움이 있음
- 2진수의 4자리와 16진수의 1자리가 1:1로 직접 대응함
- 왜 16진수인가?
- 2진수와의 상호 변환의 용이성만을 고려한다면, 8진수나 32진수도 적합함
- 2의 거듭제곱인 진법이라면, 마찬가지로 각 자릿수 간의 1:1 대응이 가능함
- 16진수에서는 한 자릿수를 나타내기 위해 4비트가 필요함
- 이 비트 수 또한 2의 거듭제곱인 경우가 여러모로 편리함
- 8진수의 경우 3비트가 되며, 2의 거듭제곱에서 벗어남
- 10진수에 가까워서 이해가 쉬움
- 2진수와의 상호 변환의 용이성만을 고려한다면, 8진수나 32진수도 적합함
- BCD Binary-coded decimal
- 2진수 4자리(16진수 1자리)로 10진수 각 자릿수를 나타내는 방법
- 0b0000(0x0) ~ 0b1001(0x9)은 0~9를 나타냄
- 예시: 0x1234는 1234를 의미함
- BCD의 장점과 단점
- 장점: 자릿수가 1:1로 대응되므로 2진수와 10진수 간의 상호 변환이 쉬움
- 단점: 0xa ~ 0xf는 사용하지 않으므로 동일한 자릿수로 표현 가능한 수의 수가 줄어듦
- 기본적으로는 낭비이므로, 현대에는 거의 사용되지 않음
- 단, 돈을 다루는 상황에서는 지금도 사용되는 경우가 있음
- 10진수에서 딱 떨어지는 수가 2진수에서는 순환소수가 되는 경우가 있음
- 예: 0.1은 2진수로 표현하면 0.0001 1001 1001 1001 1001 …
- 2진수에서는 유한한 자릿수로 표현이 불가능하므로 오차가 발생함
- 세금이나 이자 계산 등은 10진수를 전제로 규칙이 구성되어 있음
- 소비세 10% 계산 시마다 미세한 오차가 생기면 곤란함
- 이자가 미세하게 많아지거나 적어지는 것도 문제임
- 10진수에서 딱 떨어지는 수가 2진수에서는 순환소수가 되는 경우가 있음
- 2진수 4자리(16진수 1자리)로 10진수 각 자릿수를 나타내는 방법
논리회로에 의한 CPU의 구조
논리회로의 복습
- 조합 논리 회로
- 출력이 현재의 입력만으로 결정되는 논리 회로
- 순차 논리 회로
- 출력이 과거의 입력(입력 이력)에도 의존하는 논리 회로
조합 논리 회로
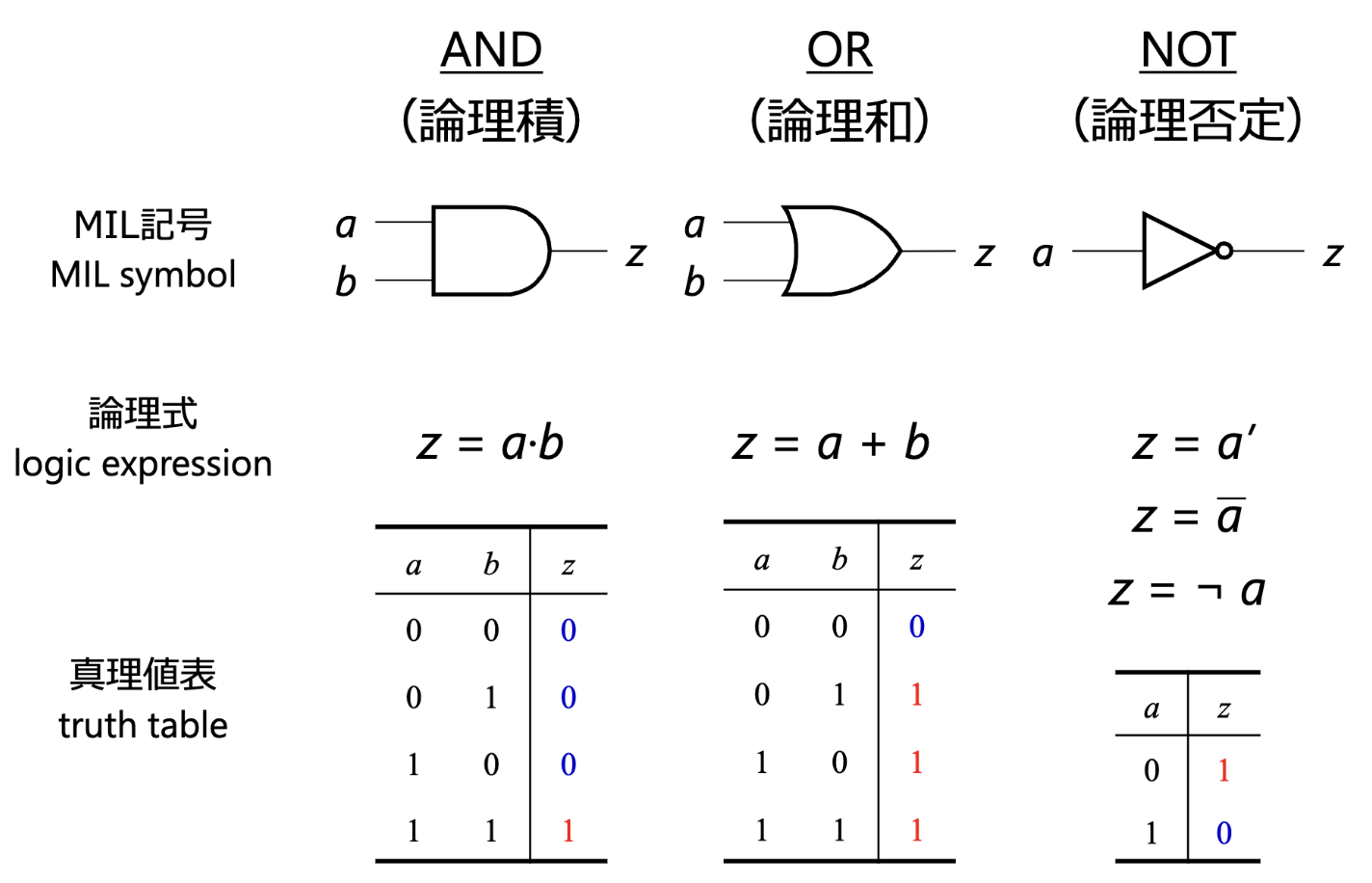
- 완전성 Completeness
- 완전 집합 Complete Set
- 해당 조합만으로 모든 논리 함수를 표현할 수 있는 논리 함수의 집합
- 완전 집합의 예시
- {AND, OR, NOT}
- {AND, NOT}
- {OR, NOT}
- {NAND}
- {NOR}
- 예를 들어, {AND, OR, NOT}을 조합하면 임의의 논리 함수를 구성할 수 있음
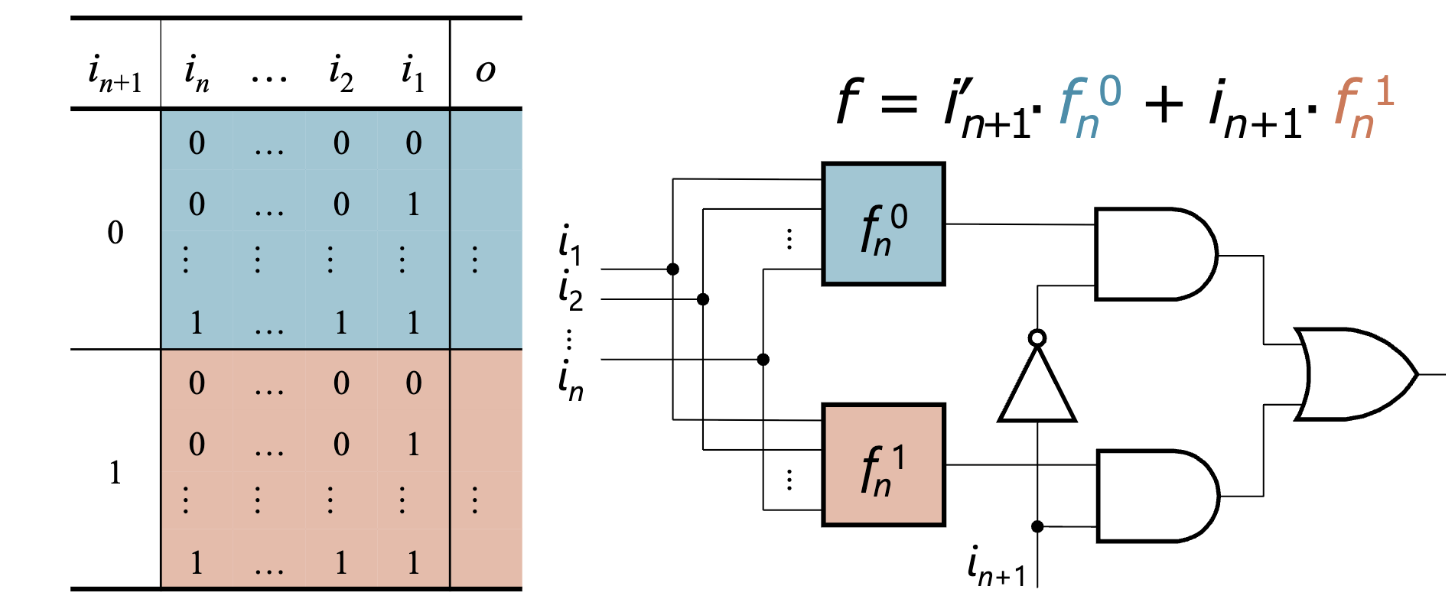
- 완전 집합 Complete Set
- 진리값 표를 이용해, 그에 대응하는 회로 그림을 작성할 수 있음
-
멀티플렉서
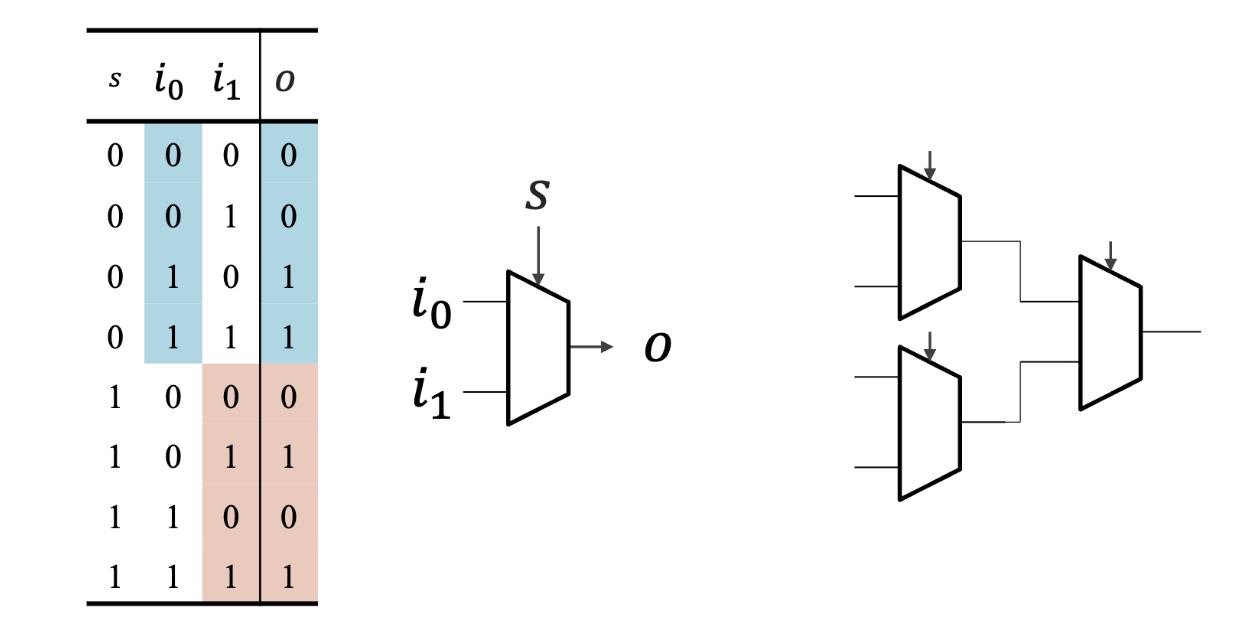
- 복수 입력으로부터 하나를 선택하는 회로
- 다음에 의해 회로의 생성이 가능함
- 2:1 멀티플렉서는 진리값표로 표현 가능함 → 회로의 작성이 가능함
- 다입력 멀티플렉서는 카스케이드 방식으로 구성하면 됨
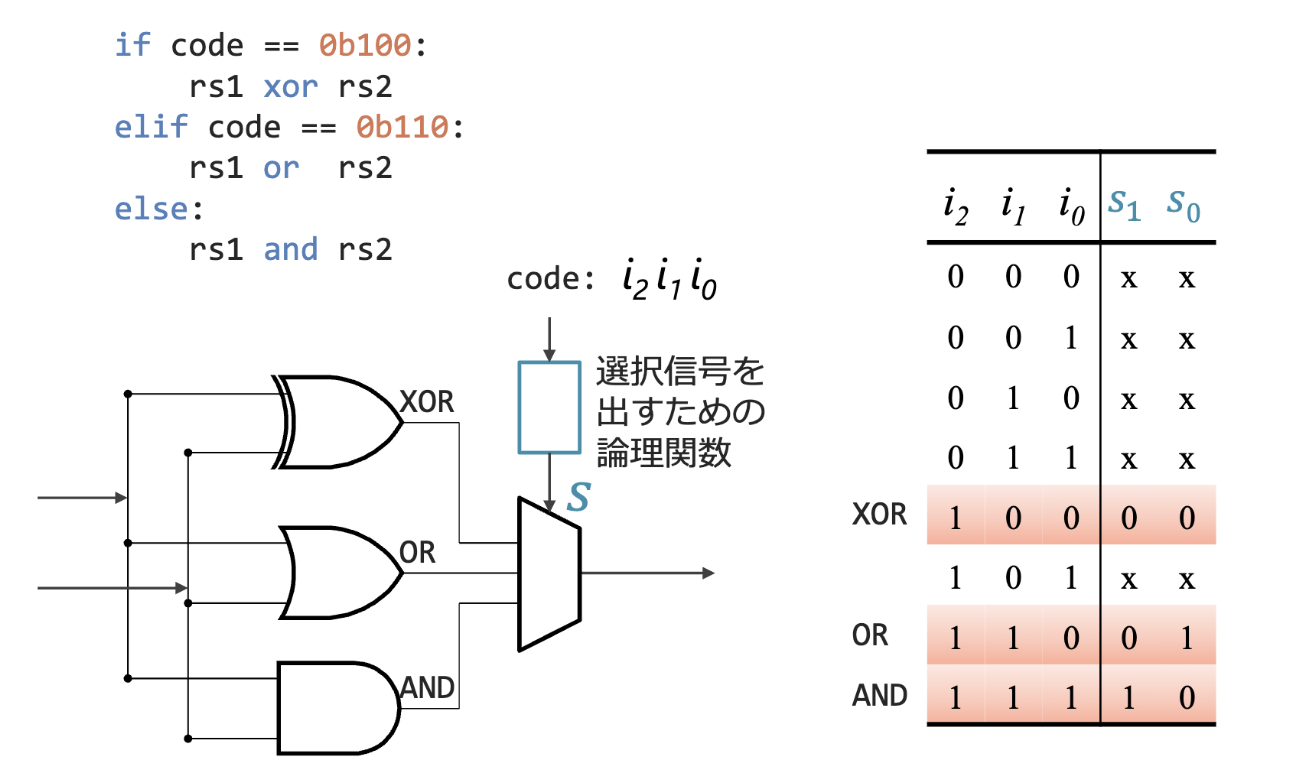
- 결국 ‘조건에 따라 다른 연산을 출력하는 회로’는
- 각 경우에 대응하는 회로를 준비하여 병렬로 배치함
- 제어 신호에 따라 멀티플렉서를 사용하여 출력을 선택함
- 위와 같은 방식으로 분해하여 AND/OR/NOT 회로로 환원 가능함

순차 논리 회로
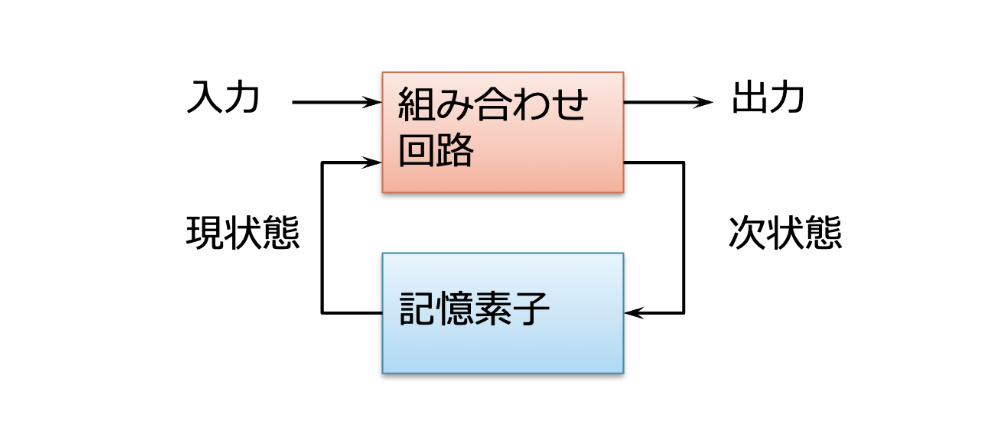
- 출력이 과거의 입력에도 의존하는 논리 회로
- 기억 소자(PC)와 조합 논리 회로로 구성됨
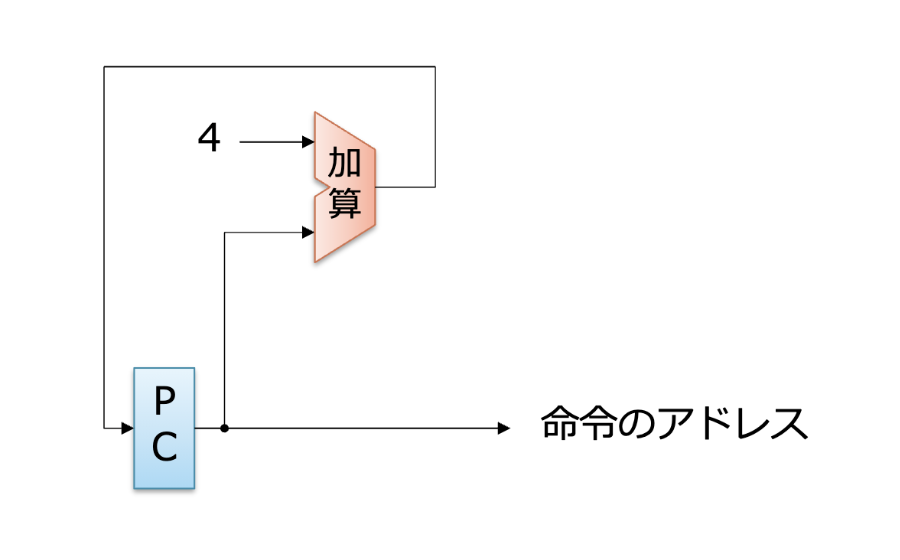
-
기억 소자의 예: D-FF(Flip Flop)
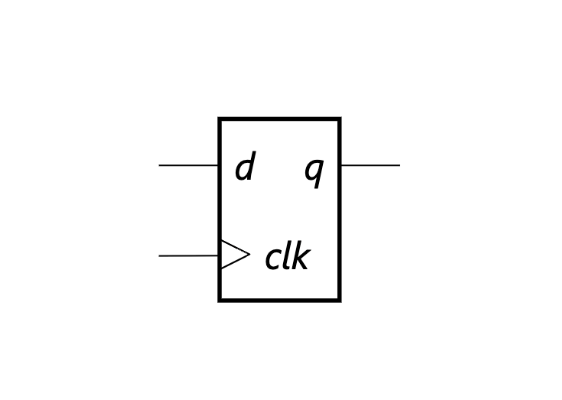
- 동작
- 클록의 상승 에지마다 d의 값이 샘플링됨
- 그 값이 다음 사이클 동안 q에서 출력됨
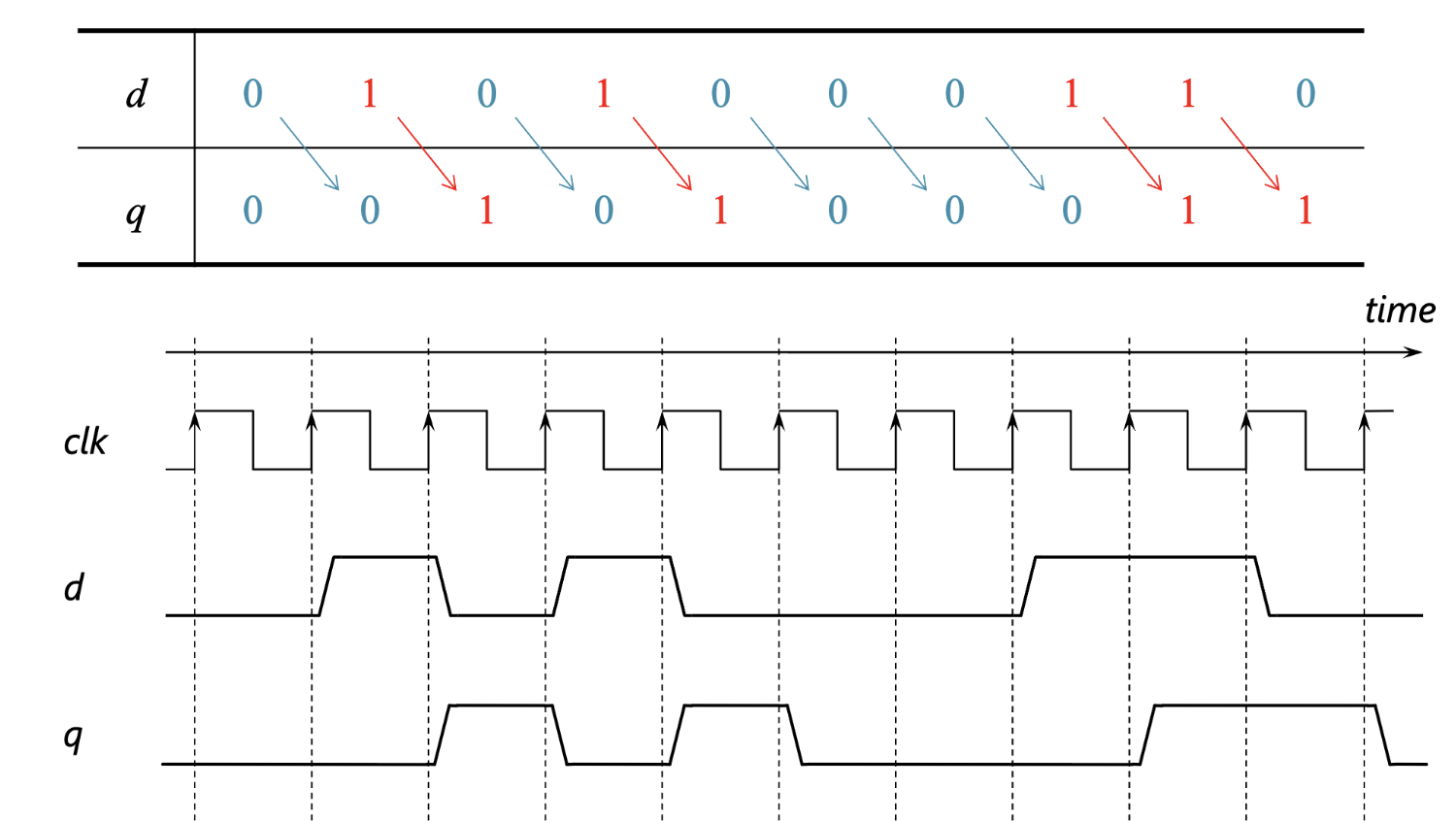
- 동작
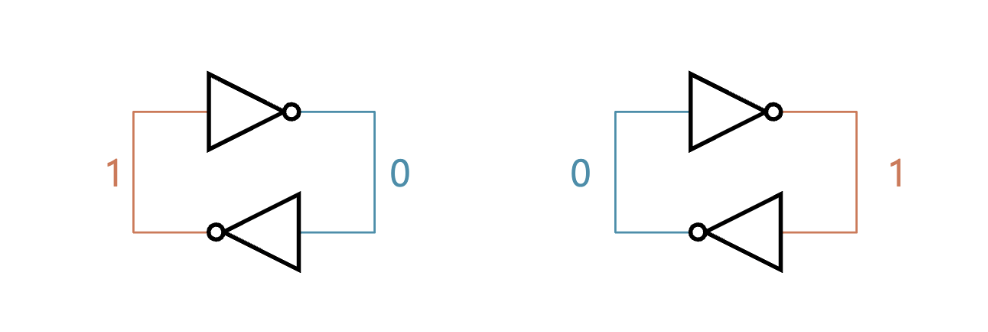
- 기억
- 두 개의 NOT 게이트를 루프로 연결한 회로에 의한 기억
- 두 가지의 안정 상태가 존재함 → 1비트를 기억함
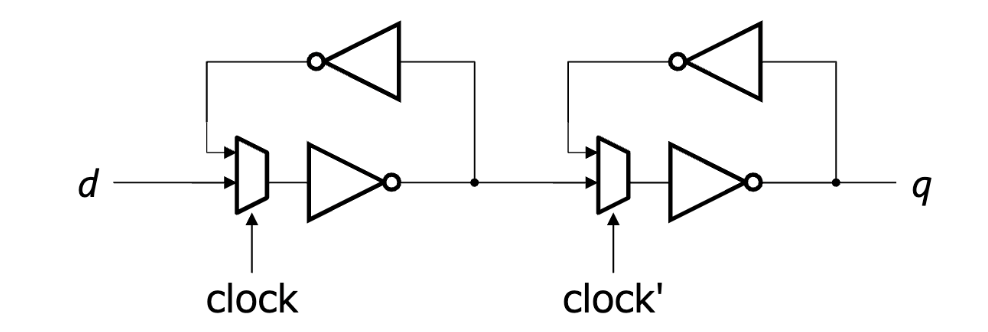
- 구조
- NOT 게이트의 루프를 2단으로 연결함
- 각 루프에는 멀티플렉서가 포함되어 있음
- 이 구조는 클록의 에지에서 기억을 갱신하기 위한 것임
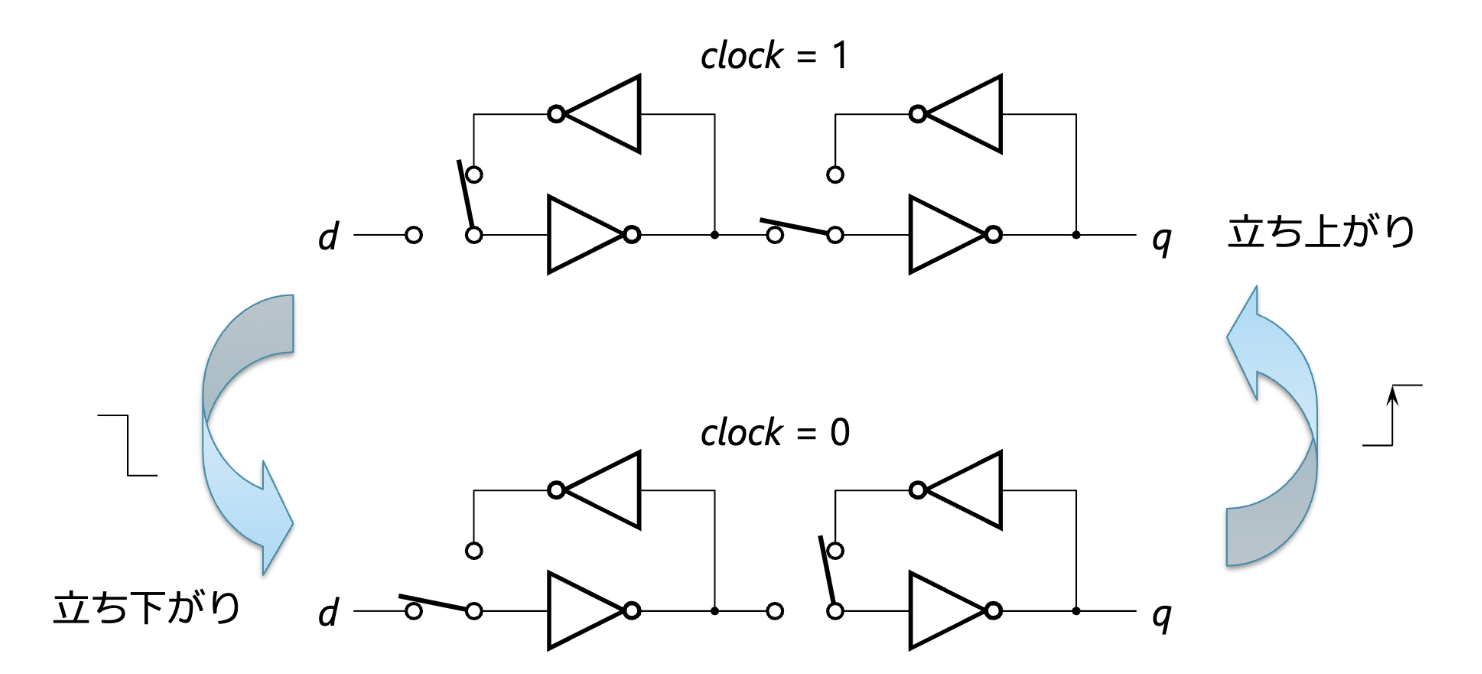
- 멀티플렉서를 전환 스위치로서 설명함
- 클록의 상승 에지마다 d의 값이 샘플링됨
- 그 값이 다음 사이클 동안 q에서 출력됨
- 메모리, 레지스터, 파일
- D 플립플롭을 필요한 만큼 나열하고, 멀티플렉서로 선택함으로써 실현 가능함
- 실제로는 더 최적화된 회로(SRAM)가 사용되는 경우가 많음
- (자세한 내용은 이후 강의에서 설명할 예정임)
- D 플립플롭을 필요한 만큼 나열하고, 멀티플렉서로 선택함으로써 실현 가능함
- 정리
- 기억 소자 또한 NOT 게이트 등의 논리 게이트로 구성됨
- 그 결과, 임의의 조합 논리 회로 및 순차 논리 회로는
- 원리적으로는 완전 집합의 요소 조합으로 환원 가능함
- 예를 들어 {AND, OR, NOT}을 조합하면 모두 구현 가능함
- 그 결과, 임의의 조합 논리 회로 및 순차 논리 회로는
- 기억 소자 또한 NOT 게이트 등의 논리 게이트로 구성됨
